dijkstra算法
算法简介
单源最短路算法
算法思想
记已经访问过的点集合为$S$,未被访问过的点集合为$T$。
算法步骤:
- 每次找到$T$中距离源点最近的点$x$
- 将$x$点加入$S$集合,此时$x$到源点的距离$dis[x]$即为最短路的距离
- 利用$x$点将集合$T$中的点到源点的距离进行更新。
步骤2中,可以利用优先队列在$O(\log n)$时间复杂度内找到$x$。
优先队列优化时间复杂度 $O(n\log n)$。
注意事项
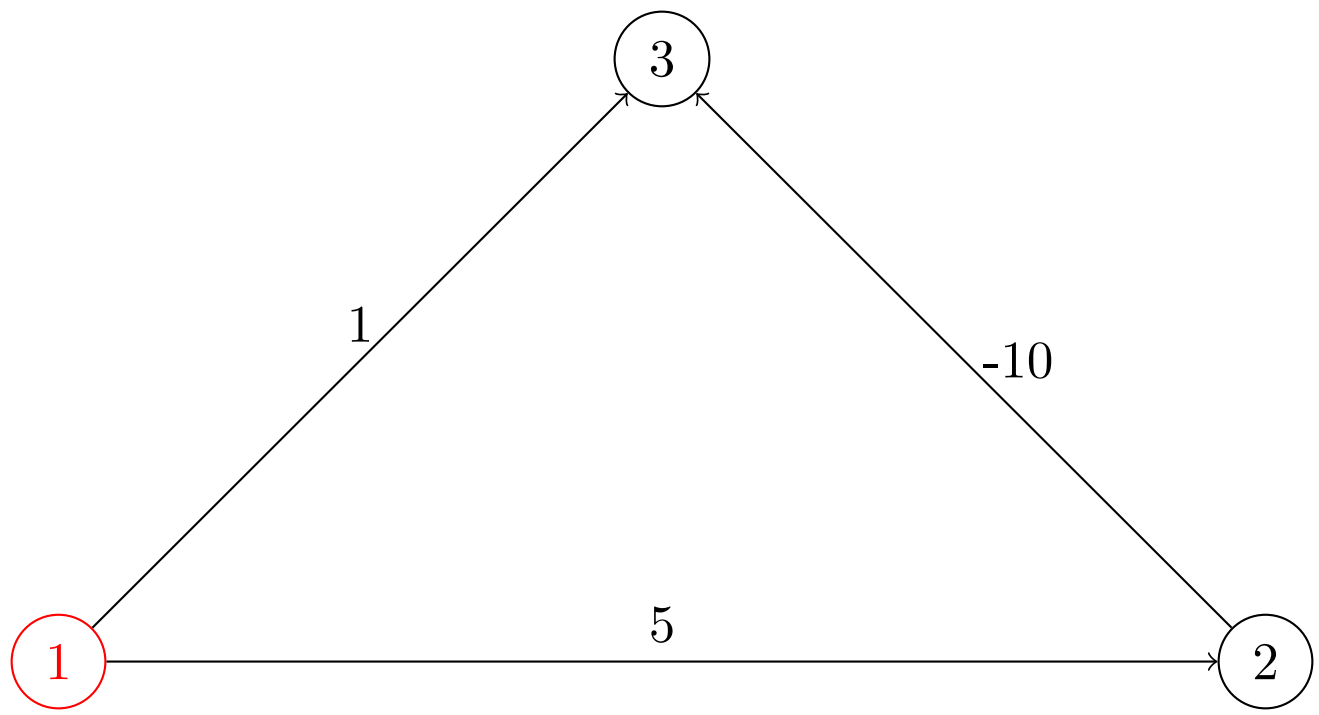
dijkstra无法处理负权边,如下图所示,dijkstra算法跑出来$dis[3] = 1$,但实际上$dis[3] = -5$。
代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#include<cmath>
#include<queue>
#define LL long long
using namespace std;
const int maxx = 2e5 + 10;
const LL inf = 1e18;
struct node{
LL id, dis;
bool operator < (const node &A) const{
return dis > A.dis;
}
};
LL n, m, s, dis[maxx];
vector<pair<LL, LL>> vec[maxx];
priority_queue<node> q;
bool vis[maxx];
void dijkstra(){
for(int i = 0; i <= n; ++i) dis[i] = inf;
dis[s] = 0; q.push((node){s, dis[s]});
while(!q.empty()){
LL id = q.top().id; q.pop();
if(vis[id]) continue;
vis[id] = 1;
for(auto u : vec[id]){
LL v = u.first, w = u.second;
if(!vis[v] && dis[v] > dis[id] + w){
dis[v] = dis[id] + w;
q.push((node){v, dis[v]});
}
}
}
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cin >> n >> m >> s;
for(int i = 1; i <= m; ++i){
int u, v, w;
cin >> u >> v >> w;
vec[u].push_back(make_pair(v, w));
}
dijkstra();
for(int i = 1; i <= n; ++i) cout << dis[i] << " ";
return 0;
}floyed 算法
算法简介
求图上任意两点最短路。
算法思路
类似动态规划思想,枚举路径上的中间节点$k$更新$dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j])$,时间复杂度:$O(n^3)$
代码
for(int k = 1; k <= n; ++k)
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= n; ++j)
a[i][j] = min(a[i][j], a[i][k] + a[k][j]);例题
题意
$n$个点,$m$条边的图$G$上,第$i$个点在时刻$t_i$才会加入图中,有$Q$次询问,每次询问$T$时刻时,$x$到$y$的最短路。
思路
每次加入一个点时不需要重新跑一遍floyed算法,只需要利用floyed算法的思想,在加入点$i$时,枚举中间节点$1$到$i-1$,更新$dis[i][*]$;再将$i$当作中间节点,更新$dis[j][k]$。
总时间复杂度:$O(n^3)$
代码
//https://www.luogu.com.cn/problem/P1119
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
const int N = 205, inf = 1e9;
int n, m, Q, t[N], a[N][N], dis[N][N];
int main(){
ios::sync_with_stdio(false); cin.tie(0);
freopen("input.in", "r", stdin);
freopen("output.out", "w", stdout);
cin >> n >> m;
for(int i = 0; i < n; ++i){
cin >> t[i];
for(int j = 0; j < n; ++j)
a[i][j] = dis[i][j] = inf;
dis[i][i] = a[i][i] = 0;
}
for(int i = 1; i <= m; ++i){
int u, v;
cin >> u >> v;
cin >> a[u][v];
a[v][u] = a[u][v];
}
t[n] = inf;
cin >> Q;
int index = 0;
while(Q--){
int x, y, T;
cin >> x >> y >> T;
while(T >= t[index]){
for(int i = 0; i < index; ++i) dis[i][index] = dis[index][i] = a[i][index];
for(int k = 0; k < index; ++k)
for(int j = 0; j < index; ++j){
dis[index][j] = min(dis[index][j], dis[index][k] + dis[k][j]);
dis[j][index] = dis[index][j];
}
for(int i = 0; i < index; ++i)
for(int j = i + 1; j < index; ++j){
dis[i][j] = min(dis[i][j], dis[i][index] + dis[index][j]);
dis[j][i] = dis[i][j];
}
++index;
}
if(dis[x][y] == inf) cout << -1 << endl;
else cout << dis[x][y] << endl;
}
return 0;
}SPFA
算法简介
单源最短路问题
算法思想
每次从队列从取出一个点,并将该点出队。用该点更新周围点的dis值,如果一个点的dis值能被更新,且这个点不在队列中,则将这个点加入队列。一直没有点的dis值能被更新,算法结束。
时间复杂度非常玄学,通常情况下$O(n\log n)$,但最坏情况下会被卡到$O(n^2)$。
虽然相比dijkstra算法,SPFA看起来死了,但是在存在负权边的情况,SPFA仍然能发挥作用。而且SPFA还可以判断图中是否有负权环,如果一个点进队超过$n$次,则图中一定存在一个负权环。
代码
queue<int> q;
bool spfa(int s){
for(int i = 1; i <= n; ++i){
dis[i] = inf;
p[i] = 0;
}
dis[s] = 0; q.push(s);
while(!q.empty()){
LL u = q.front(); q.pop();
p[u] = 0; vis[u] = 1;
for(auto x : edge[u]){
LL v = x.first, w = x.second;
if(dis[v] > dis[u] + w){
dis[v] = dis[u] + w;
if(!p[v]){
if(num[v] > n) return 0;
q.push(v);
++num[v];
p[v] = 1;
}
}
}
}
return 1;
}
