后缀数组(Suffix Array)

字符串

发布日期: 2022-09-11

更新日期: 2022-09-17

文章字数: 2.2k

阅读次数:

名词解释

字符串的后缀k	下标从k开始一直到原串末尾的字符子串
LCP	多个串的最长公共前缀
后缀数组(SA)	一个串所有后缀按字典序排序，$SA[i] = k$表示字典序排名为i的后缀起始位置为k
rank数组	SA数组的逆数组，$rk[i] = k$表示后缀i的排名为k
height数组	后缀sa[i - 1]和后缀sa[i]的LCP
h数组	辅助数组，便于height的求解，定义为$h[i] = height[rk[i]]$

下图以“aabaaab”为例，用来理解sa数组与rk数组：

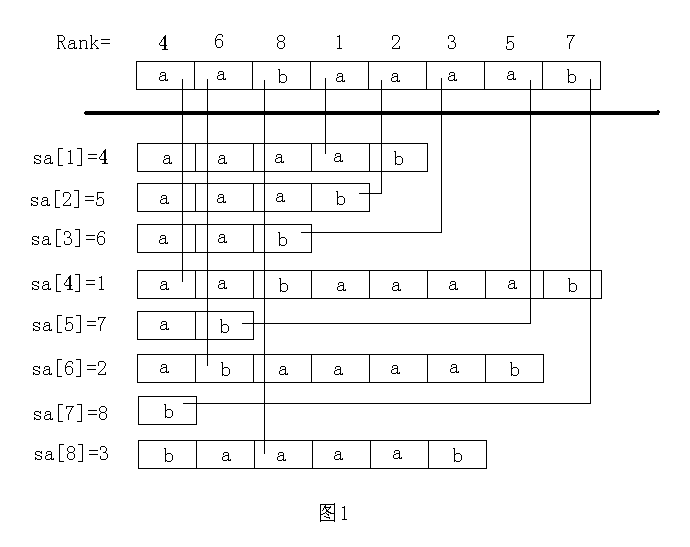
images

后缀排序(计算SA)

好的博客

OIWIKI

朴素算法 $O(n^2\log n)$

暴力的做法：对于长度为n的字符串，取出n个后缀直接sort，时间复杂度为$O(n^2\log n)$。

倍增思想 $O(n\log^2n)$

如下图所示：

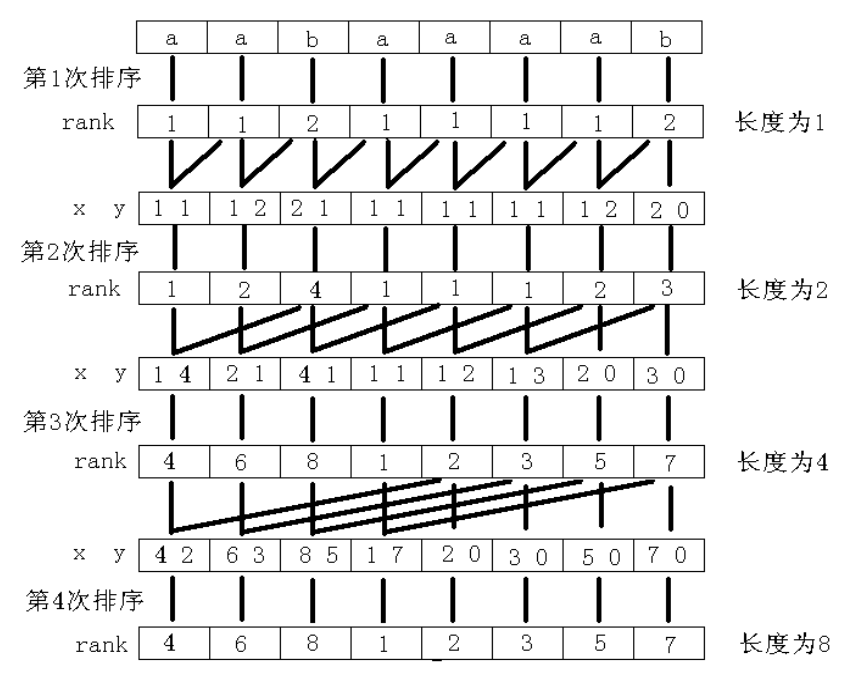
第$i$次排序时，计算每个后缀子串前$2^i$长度的前缀的$SA_i$。

在第$i - 1$次排序后，已经知道了每个后缀子串$2^{i-1}$长度的前缀$SA_{i - 1}$，于是本算法的思想就是用$SA_{i - 1}$计算出$SA_{i}$。

当前已经知道每个后缀的前$2^{i - 1}$前缀之间的相对大小，扩展到$2^i$长度时，相当于在原来的大小x上，添加一个第二关键字y，就构成一对pair型变量，如果直接对这些pair变量sort，就可以新的相对关系，时间复杂度为$O(n\log^2n)$。

基数排序 $O(n\log n)$

在倍增算法中，对于每次倍增都对每个后缀计算出一个pair变量，再sort比较大小，这么做感觉很吃亏，遗漏了很多条件。

因为我们知道的是后缀直接的大小关系，也就是说每个pair变量的关键字都是在$[1, n]$。那么可以考虑是否能够进行桶排？因为有两个关键字，那么考虑一种类似桶排的方式。

我们先统计第二关键字的相对大小。$y[i]=k$表示第二关键字排名为$i$的为后缀$k$。

因为存在一部分位置不能再往后扩展$2^{i-1}$长度，也就是说接上了一个空串，空串的优先级最高，则第二关键字排名靠前：

int num = 0;
for(int i = n - k + 1; i <= n; ++i) y[++num] = i;

之后按照$SA_{i-1}$的排名顺序，依次计算$y$数组，$sa[i] - k$表示该第二关键字对应的前缀下标：

for(int i = 1; i <= n; ++i) if(sa[i] > k) y[++num] = sa[i] - k;

接着，按照第一关键字，统计每个第一关键字出现的次数，和最高的排名：

for(int i = 1; i <= m; ++i) c[i] = 0;
for(int i = 1; i <= n; ++i) ++c[x[i]];
for(int i = 1; i <= m; ++i) c[i] += c[i - 1];	//第一关键字i对应的最大的排名为c[i]

最后，按照第二关键字的逆序求出$SA_i$：

for(int i = n; i >= 1; --i){
       sa[c[x[y[i]]]--] = y[i];
       y[i] = 0;
   }

由于求出了$c[i]$数组，我们保证了第一关键字不同的后缀之间的排名一定会满足关系，例如第一关键字1出现了2次，2出现了3次，则$c[1] = 2, c[2] = 5$，那么第一关键字为1的后缀对应的排名一定在$[1,2]$，而第一关键字为2的后缀对应的排名一定在$[3, 5]$。既然第一关键字能够保证正确，那么第一关键字相同时，重点在保证第二关键字能正确进行排序，采用y数组逆序枚举则可以保证这一需求。

求出$SA_i$后，为了下一轮的求解，应该利用新的$SA_i$求出第一关键字排序：

swap(x, y);
x[sa[1]] = num = 1;
for(int i = 2; i <= n; ++i)
	x[sa[i]] = (y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k]) ? num : ++num;

完整代码

/*************************************************************************
	> File Name: 1.cpp
	> Author: Knowledge_llz
	> Mail: 925538513@qq.com 
	> Blog: https://www.cnblogs.com/Knowledge-Pig/ 
	> Created Time: 2022/4/3 22:09:18
 ************************************************************************/

#include<bits/stdc++.h>
#define LL long long
#define endl '\n'
using namespace std;
const int maxx = 2e6 + 10;
int n, m, sa[maxx], x[maxx], y[maxx], c[maxx];
char s[maxx];
void build_sa(){
	for(int i = 1; i <= n; ++i) ++c[x[i] = s[i]];
	for(int i = 1; i <= m; ++i) c[i] += c[i - 1];
	for(int i = n; i >= 1; --i) sa[c[x[i]]--] = i;
	for(int k = 1; k <= n; k <<= 1){
		int num = 0;
		for(int i = n - k + 1; i <= n; ++i) y[++num] = i;
		for(int i = 1; i <= n; ++i) if(sa[i] > k) y[++num] = sa[i] - k;
		for(int i = 1; i <= m; ++i) c[i] = 0;
		for(int i = 1; i <= n; ++i) ++c[x[i]];
		for(int i = 1; i <= m; ++i) c[i] += c[i - 1];
		for(int i = n; i >= 1; --i) sa[c[x[y[i]]]--] = y[i];
		for(int i = 1; i <= n; ++i) y[i] = x[i];
		x[sa[1]] = num = 1;
		for(int i = 2; i <= n; ++i)
			x[sa[i]] = (y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k]) ? num : ++num;
		if(num == n) break;
		m = num;
	}
}
int main(){
	ios::sync_with_stdio(false); cin.tie(0);
#ifndef ONLINE_JUDGE
	freopen("input.in", "r", stdin);
	freopen("output.out", "w", stdout);
#endif
	cin >> s + 1;
	n = strlen(s + 1);
	m = 122;
	build_sa();
	for(int i = 1; i <= n; ++i) cout << sa[i] << " ";
	return 0;
}

最长公共前缀(LCP)

得到了后缀数组之后，我们还可以进一步利用后缀数组对求出两个后缀的最长公共前缀(LCP)。但光有$sa$数组，能做的事情并不多，还需要得到$rk$数组和$height$数组，$rk[i]$代表后缀$i$的字典序排名，$height[i]$表示$sa[i]$与$sa[i - 1]$的LCP。对于后缀$j,k$的LCP长度等于$min\{height[rk[j]] + 1,height[rk[j] + 2]\cdots,height[rk[k]]\}$，这个结论联系后缀树很好理解。

计算height数组

$rk$数组可以由$sa$数组直接导出，剩下的问题就是求$height$数组。

朴素算法 $O(n^2)$

对于每个$height[i]$都进行依次字符串匹配，依次匹配的时间复杂度为$O(n)$，总时间复杂度为$O(n^2)$。

辅助数组 $O(n)$

构造辅助数组$h[i] = height[rk[i]]$，$h[i]$的意义可以表示为后缀$i$与排在后缀$i$的前一个后缀的LCP值。$h[i]$有一个神奇的性质：$h[i] \geq h[i - 1] - 1$，于是可以从$h[i],h[i + 1]\cdots h[n]$递推计算，每次不需要重新进行匹配，如以下代码所示：

int rk[maxx], height[maxx], k = 0;
void get_height(){
	for(int i = 1; i <= n; ++i) rk[sa[i]] = i;
	for(int i = 1; i <= n; ++i){
		if(rk[i] == 1) continue;
		if(k) --k;
		int j = sa[rk[i] - 1];
		while(i + k <= n && j + k <= n && s[i + k] == s[j + k]) ++k;
		height[rk[i]] = k;
	}
}

因为变量$k$每次循环中只会减少1，最大为$n$，故时间复杂度为$O(n)$。

关于结论$h[i] \geq h[i - 1] - 1$的证明：

假设排在后缀$i-1$之前的是后缀$k$，后缀$k$与后缀$i -1$的LCP长度为$h[i-1]$；那么同时删去两个后缀的首字母，则有后缀$k + 1$与后缀$i$的LCP长度为$h[i- 1] - 1$，且后缀$k + 1$一定会排在后缀$i$之前，假设排在后缀$i$的前一个后缀为后缀$p$：

$\because rk[k + 1] \leq rk[p] < rk[i]$

$\therefore$ 联系后缀树，后缀$k+1$与后缀$i$的LCP一定不小于$h[i - 1] - 1$

即 $h[i] \geq h[i - 1] - 1$

完整代码

/*************************************************************************
	> https://www.luogu.com.cn/problem/P3809
	> Created Time: 2022/4/3 22:09:18
 ************************************************************************/

#include<bits/stdc++.h>
#define LL long long
#define endl '\n'
using namespace std;
const int maxx = 2e6 + 10;
int n, m, sa[maxx], x[maxx], y[maxx], c[maxx];
char s[maxx];
void build_sa(){
	for(int i = 1; i <= n; ++i) ++c[x[i] = s[i]];
	for(int i = 1; i <= m; ++i) c[i] += c[i - 1];
	for(int i = n; i >= 1; --i) sa[c[x[i]]--] = i;
	for(int k = 1; k <= n; k <<= 1){
		int num = 0;
		for(int i = n - k + 1; i <= n; ++i) y[++num] = i;
		for(int i = 1; i <= n; ++i) if(sa[i] > k) y[++num] = sa[i] - k;
		for(int i = 1; i <= m; ++i) c[i] = 0;
		for(int i = 1; i <= n; ++i) ++c[x[i]];
		for(int i = 1; i <= m; ++i) c[i] += c[i - 1];
		for(int i = n; i >= 1; --i){ sa[c[x[y[i]]]--] = y[i]; y[i] = 0; }
		swap(x, y);
		x[sa[1]] = num = 1;
		for(int i = 2; i <= n; ++i)
			x[sa[i]] = (y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k]) ? num : ++num;
		if(num == n) break;
		m = num;
	}
}
int rk[maxx], height[maxx], k = 0;
void get_height(){
	for(int i = 1; i <= n; ++i) rk[sa[i]] = i;
	for(int i = 1; i <= n; ++i){
		if(rk[i] == 1) continue;
		if(k) --k;
		int j = sa[rk[i] - 1];
		while(i + k <= n && j + k <= n && s[i + k] == s[j + k]) ++k;
		height[rk[i]] = k;
	}
}
int main(){
	ios::sync_with_stdio(false); cin.tie(0);
#ifndef ONLINE_JUDGE
	freopen("input.in", "r", stdin);
	freopen("output.out", "w", stdout);
#endif
	cin >> s + 1;
	n = strlen(s + 1);
	m = 122;
	build_sa();
	for(int i = 1; i <= n; ++i) cout << sa[i] << " ";
    get_height();
	return 0;
}