信息检索导论笔记（二）

信息检索

Information Retrieval

发布日期: 2022-11-05

更新日期: 2022-11-07

文章字数: 5k

阅读次数:

索引压缩

统计特性

压缩意义：

节省磁盘空间
增加高速缓存 (caching)技术的利用率
加快数据从磁盘到内存的传输速度

统计规律：

30定律（rule of 30）：出现频率最高的30个词在书面文本占30%的出现比例
Heaps定律：词项数目估计与文档集大小符合函数 $M=kT^b$，$M$是词项数目，$T$是文档长度，$k,b$典型取值：$30\leq k\leq 100, b\approx 0.5$
Zipf定律：出现频率排名第i多的词项的文档集频率$cf_i$满足 $cf_i\propto \frac{1}{i}$。即出现第二多的词项出现次数是出现最多词项次数的一半。

词典压缩方法

将词典看成单一字符串的压缩方法

通常整个词典采用定长数组来存储，假定对每个词项采用20B的固定长度（英文单词很少有长度大于20B的词），文档频率采用4B存储，词项倒排表的地址指针采用4B存储，对于400000个词的词典需要$400000\times(20 + 4 + 4) = 11.2MB$。

采用定长方法存储很容易造成空间浪费，为了避免浪费，可以将所有词项存成一个长字符串并给每个词项增加一个定位指针，由于词项平均长度为12B，每个定位指针消耗3B，$400000\times (8 + 3 + 4 + 4)=7.6MB$。

按块存储

将长字符串的词项分组变成大小为k的块，对每个块只保留第一个词项的指针，并用一个额外字节将每个词项的长度存储在首部。因此对于每个块可以减少k-1个词项指针，即9B，但是需要额外的kB来保存k个词项长度，上面方法的7.6MB可以降低到7.1MB。

显然，k越大，压缩率也越高，但是词项查找速会降低，必须要保持压缩和查找速度之间的平衡。

其它压缩技术

前端编码 (front coding)：按照词典顺序排序的连续词项之间往往具有公共前缀，公共前缀被识别出来之后，后续的此项中便可以使用一个特殊的字符来表示这段前缀。

最小完美哈希：该哈希函数将M个词项映射到[1,…,M]上，并且不会发生任何冲突。但是当插入新词项时，显然会发生冲突，此时不能对原有的完美哈希结果进行增量式修改，而只能重新构造新的完美哈希函数。因此，完美哈希的方法无法在动态环境下使用。

倒排记录表的压缩

思想：高频词出现的文档ID序列值之间相差不大，可以采用存储间隔值的方式，对于小数字的存储可采用比大数字更短的编码方式

两类方法：对间距采用最短字节方式或位方式

可变字节码

字节的后7位是间距的有效编码区，而第1位是延续位（continuation bit）。如果该位为1，则表明本字节是某个间距编码的最后一个字节，否则不是。

要对一个可变字节编码进行解码，可以读入一段字节序列，其中前面的字节的延续位都为0，而最后一个字节的延续位为1。

可以应用于32位字、16位字等，编码单位长，位操作次数越少，压缩率下降；编码单位短，位操作次数多，压缩率上升。合理现在编码单位，在压缩率和解压缩速度上平衡。

$\gamma$编码

一元编码（unary code)：数n表示为n个1后面加个0的字符串。

对于一个很大的数，一元编码会长。为了解决这个问题，$\gamma$编码将数n表示成长度和偏移两个值，偏移则表示为去掉二进制下最高位的1剩下的字符串，长度则表示二进制表示下长度减1后的一元编码。例如13(1101)表示为偏移(101)、长度(1110)。这样偏移部分长度$\lfloor\log n\rfloor$，长度部分$\lfloor\log n\rfloor + 1$。

对于$\gamma$编码解码，首先读入一元编码，直到读到0结束，读完一元编码，就可以知道偏移部分长度，再读偏移部分即可。

对于离散概率分布P，它的熵$H(P)$：
$$
H(P) = -\sum_{x\in X}P(x)\log_2P(x)
$$
其中$X$表示所有需要编码的数字集合。

有人证明了，对于$1<H(P)<\infty$最优编码长度期望$E(L)$与$H(P)$满足：
$$
\frac{E(L_\gamma)}{H(P)}\leq 2 + \frac{1}{H(P)}\leq 3
$$
对于任意概率分布，$\gamma$编码能够达到最优编码的2倍左右，也被称为通用性编码。

两个特性：

前缀无关性：一个$\gamma$编码不会是另一个$\gamma$编码的前缀
参数无关系：不需要存储和检索参数

文档评分、词项权重计算及向量空间模型

参数化索引及域索引

元数据（metadata）：和文档有关的特定形式的数据，如文档作者、标题、出版日期

字段（field）：元数据包含字段信息，文档创建日期、文档格式、文档标题有时可以看作字段信息

域（zone）：和字段相似，但内容可以是自由文本

域索引：词典常常来自固定的词汇表，而在域索引中词典应该收集来自域中自由文本的所有词汇

实际上可以通过对域进行编码来减少上述索引中词典的规模。当词典大小为主要关注目标是，这种编码方式就非常有用（比如我们要将词典放入内存）。采用这种编码得另外一个重要原因就是它能支持域加权评分（weighted zone scoring）技术的使用。

域加权评分

每篇文档有$l$个域，其对应的权重为$g_1,g_2…g_l\in[0,1]$，满足$\sum g_i = 1$。

令$s_i$为查询文档的第$i$个域的匹配得分（1为匹配上，0为未匹配）。域加权评分方法可以定义为：
$$
\sum_{i=1}^l g_is_i
$$
该方法有时也称为排序式布尔检索（ranked Boolean retrieval）。

考虑两个词项$q_1$,$q_2$，之间存在AND关系，若出现在文档同一域则得分为1，否则为0。计算算法如下：

权重学习

对于不同域的权重，可以由专家标定，或者用户指定。目前越来越倾向于机器学习方式从人工标注的训练数据中学习权重。（见课本15章)

词项频率及权重计算

概念	定义
词袋模型（bag of word model）	词项在文档中出现次序被忽略，但是出现的次数非常重要。如，John is quicker than Marry等价于Marry is quicker than John。
词项频率（term frequency）	$tf_{t,d}$，表示对于词项t在文档d中的出现次数
文档集频率（collection frequency）	$cf_t$，词项在文档集中出现的次数
文档频率（document frequency）	$df_t$，表示出现t的所有文档数目
逆文档频率（inverse document frequency）	$idf_t=\lg\frac{N}{df_t}$
tf-idf权重	$tf\text{-}idf_{t,d}=tf_{t,d}\times idf_t$：

理解tf-idf权重：

当t在少数文档中多次出现（$tf$大，$df$小，$idf$大），权重取值大（此时能够对这些文档提供最强的区分能力）
当t在一篇文档中出现次数很少，或者在很多文档中出现（$tf$小，$df$大，$idf$小），权重取值次之
如果t在所有文档中出现，那么权重取值为0（$idf=0$)

于是可以将每个文档看成一个向量，每个分量对应一个词项，分量值用tf-idf权重表示，于是可以对每个查询计算文档的得分：
$$
Score(q,d) = \sum_{t\in q} tf\text{-}idf_{t,d}
$$

向量空间模型

将每篇文档d看作一个向量$\vec{V}(d)$，如何计算两篇文档的相似度呢？一个简单的想法是求两篇文档对应向量差的大小，然而内容相似的文档，可能因为文档长度差异导致向量差很大。

为弥补以上问题，计算文档相似度常规方法是余弦相似度：
$$
sim(d_i,d_2) =\frac{\vec{V}(d_1)\cdot\vec{V}(d_2)}{|\vec V(d_1)|\cdot \vec V(d_2)}
$$
可以直接将文档归一化，$\vec v(d) = \frac{\vec V(d)}{|V(d)|}$，则有
$$
sim(d_i,d_2) =v(d_1)\cdot v(d_2)
$$

查询向量

将查询也看作向量$\vec v(q)$，计算每篇文档的得分：
$$
Score(q,d) =\frac{\vec{V}(d)\cdot\vec{V}(q)}{|\vec V(d)|\cdot \vec V(q)}=v(q)\cdot v(d)
$$
由于计算每篇文档与查询的余弦相似度代价太大，一般用启发式策略。

向量相似度计算

其他tf-idf权重计算方法

tf的亚线性尺度变换方法：一个词项在文档出现20次，但重要性不可能是出现1次的20倍

基于最大值的tf归一化：采用文档中最大的词项频率对所有词项归一化

其中a表示阻尼系数，主要起平滑作用

不同权重计算表示与方法

一个完整搜索系统中评分计算

非精确返回前k篇文档的方法

非精确的好处：

显著降低输出前K篇文档所需要的计算复杂度，同时并不让用户感觉到前K个结果的相关度有所降低。
从用户的角度看，给定查询情况下，余弦相似度计算得分最高的K篇文档在很多情况下不一定就是最好的K篇文档，余弦相似度只不过是用户所感觉到的相似度的一个替代品。

策略：

(1)找到一个文档集合A，它包含了参与最后竞争的候选文档，其中 $K<∣A∣≪N$ 。A不必包含前K篇得分最高的文档，但是它应该包含很多和前K篇文档得分相近的文档。

(2)返回A中得分最高的K篇文档。

索引去除技术

对于一个包含多个词项的查询来说，我们可以仅仅考虑那些至少包含一个查询词项的文档，于是可以考虑使用如下的启发式方法。

只考虑那些词项的idf值超过一定阈值的文档
- 那些低idf值词项的倒排记录表往往比较长，如果将它们剔除，那么需要计算余弦相似度的文档数目将大大减少。
- idf值低的词项也可以看成停用词，它们对评分结果没有什么贡献。
只考虑包含多个查询词项（一个特例是包含全部查询词项）的文档
- 仅考虑对那些包含较多（或全部）查询词项的文档进行计算。
- 风险：如果仅仅对这些文档进行相似度计算，那么很有可能最后的候选结果文档数目少于K个。

胜者表

基本思路：

对每个词项t，预先计算出r个最高权重文档，其中r的值需要预先给定。
给定查询q，对查询q中所有词项的胜者表求并集，生成集合$A$。
只有集合$A$中的文档参与最后余弦相似度计算

一个可能的问题：r的选择在构建索引前就确定，而取决于应用本身的K值需要接受到查询才能确定。因此，可能会遇到集合$A$元素个数少于K的情况。

另外，没必要将所有词项r值设为相同，对于罕见词项r值可以适当增大。

静态得分和排序

每篇文档有一个与查询无关的静态得分$g(d)$，往往取值0到1之间。对于Web上文档，$g(d)$可以基于用户正面评价次数定义。

一篇文档的最后得分为：
$$
net\text{-}score(q,d) =g(d)+\frac{\vec{V}(d)\cdot\vec{V}(q)}{|\vec V(d)|\cdot \vec V(q)}
$$
将所有文档按照$g(d)$大小降序排列重新构建倒排表。

对胜者表扩展：

对于精心选择的r值，对每个词项t构建全局胜者表，其中包含$g(d)+tf\text{-}idf_{t,d}$得分最高的r篇文档
胜者表本身则向所有的倒排记录表一样，都采用统一的排序方式（使用文档ID或者静态得分值）
于是，当查询提交以后，只需要对全局胜者表的并集中的文档计算器最后得分

另一种思路：

每个词项，维持两个无交集的倒排表，每个表按照$g(d)$排序
第一张表称为高端表，由最高的tf值文档组成
第二张表称为低端表，由剩下包含t的文档组成
对于查询，优先对高端表进行计算；如果高端表不足K篇，再对低端表计算。

影响度排序

将每个词项t对应的所有文档按照$tf_{t,d}$值降序排列，不同词项倒排表排序方式则不统一，不能并发地扫描多个倒排表计算文档得分。

降低计算文档的数目方法：

对某个查询词项t对应的倒排记录表从前往后扫描，设定阈值，当$tf_{t,d}$低于阈值则停止或者扫描固定r篇后停止
优先处理得分贡献大的词项，当词项改变值达到最小限度时，忽略剩下词项

簇剪枝方法

先对文档向量聚类进行预处理操作，步骤如下：

从N篇文档中随机选择$\sqrt N$篇文档，称为leader集合
对于每篇不属于leader集合的文档，计算最近的leader

查询处理如下：

给定查询q，通过与$\sqrt N$个leader计算余弦相似度，找出最近的leader $L$
候选集合A包括$L$及其follower，然后对A计算余弦相似度

还可以另外引入参数$b_1,b_2$，每个follower可以分配给$b_1$个leader，每次查询可以找$b_2$个leader。

层次型索引

可以按照tf值不同，将索引分为多层。例如，第一层tf阈值为20，第二层tf阈值为10。

查询词项的邻近性

用户往往希望返回的文档中大部分或者全部查询词汇距离比较近，因为这表明返回文档具有聚焦用户查询意图的文本。

令文档d中包含所有查询词项的最小窗口大小为w，其取值为窗口内词的个数。

直观上，w越小，文档d和查询匹配程度越高。

这种基于邻近性加权的评分方法背离了余弦相似度计算方法，更接近于Google搜索引擎使用的软合取语义。

软合取（soft conjunctive）：指的是在对一个包含多个词项的查询进行检索时，检索中的文档中只要出现大部分查询词项即可，并不要求出现全部查询词项。

查询分析及文档评分函数设计

通常情况下，会有一个查询分析器（query parser）将用户输入的关键词转换成带操作符的查询，该查询能够基于底层的索引结构进行处理。有时，这种处理过程可能需要基于底层索引结果对多个查询进行处理，比如，查询分析器可能会产生如下的一系列查询。

(1)将用户输入的查询字符串看成一个短语查询。

(2)如果包含短语的文档数目过少，那么会将原始查询看成多个查询短语。

(3)如果结果仍然很少，那么重新利用向量空间模型求解，这时候认为多个查询词项是独立的。

特别地，一篇文档可能在上述的多个步骤结果列表中出现。这是要求有一个综合得分函数能够融合不同来源的得分。

搜索系统的组成

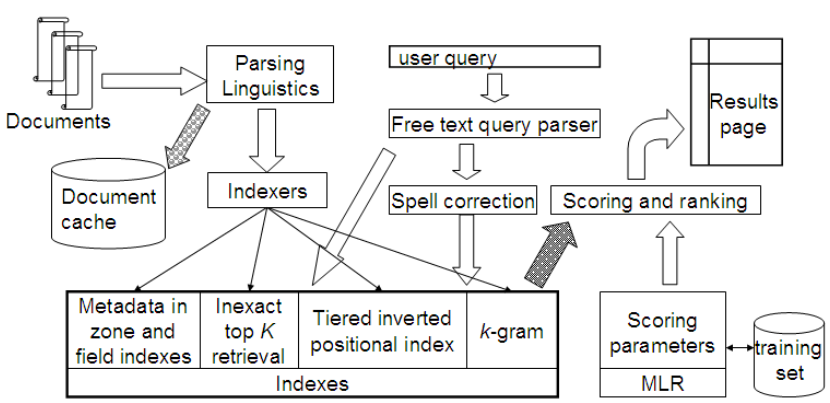
向量空间模型对各种查询操作的支持

布尔查询

在用户角度，将向量空间模型和布尔查询融合并非易事：

一方面，向量空间查询的处理基本上是证据累加（evidence accumulation）的方式，几多个查询词项的出现会增加文档的得分；
另一方面，布尔检索需要用户指定一个表达式，通过词项的出现与不出现的组合方式来选择最终的文档，文档之间并无次序可言。

数学领域实际上存在一种称为p范式（p-norm）的方法，可用于融合布尔和向量空间查询，但目前还没有实际系统这样做。

通配符查询

通配符查询和向量空间查询需要不同的索引结构来完成。

如果搜索引擎允许用户在自由文本查询中同时给定通配符，那么就可以把查询中的通配符解释成向量空间模型中的一系列查询词项，然后将所有查询词项加入到查询向量中去。

最后，上述向量空间查询按照通常的方式进行处理，结果文档评分并排序输出。

最终文档的精确排序主要取决于不同词项在文档中的相对权重。

短语查询

用于向量空间方法的索引通常并不能用于短语查询的处理。

信息检索的评价

无序检索指标

正确率（Precision，记为P）是返回的结果中相关文档所占的比例

召回率（Recall，记为R）是返回的相关文档占所有相关文档的比例

精确率（Accuracy，记为Acc）是文档集中所有判断正确的文档所占的比例

$$ ACC=\frac{tp + tn}{tp + fp+fn+tn} $$ 为什么精确率指标不好？

绝大多数情况，信息检索数据极不平衡，超过99.9%的文档是不相关的。如果将所有文档标注为不相干，显然不能让用户满意，但精确率很高，即假阳率很高

通常采用正确率和召回率度量效果，一个融合正确率和召回率的指标是F值：
$$
F=\frac{1}{\alpha\frac{1}{P}+(1-\alpha)\frac{1}{R}}=\frac{(\beta^2+1)PR}{\beta^2P+R}
$$
其中， $\beta^2=\frac{1-\alpha}{\alpha}$

当$\beta=1$时，计算公式为
$$
F_{\beta=1}=\frac{2PR}{P+R}
$$
当$\beta>1$表示强调召回率，当$\beta<1$表示强调正确率。

有序检索指标

无序检索指标不考虑返回文档之间的顺序，有序检索还要考虑返回的文档之间的次序。

很自然地，将前面k(k=1,2,3…)个检索结果组成返回文档子集，对于每个集合都可以得到正确率和召回率，可以描点成正确率-召回率曲线：

通常，采用11点插值平均正确率，取0.0、0.1…1.0等11个召回率水平，绘制曲线：